2024. 2. 10. 11:48ㆍIT/TIL
오늘의 TIL은 프로그래머스의 문제인 2개 이하로 다른 비트에 관한 내용이다.
문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/77885
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제에 대해서 설명하면,
양의 정수 x에 대한 함수 f(x)가 아래와 같이 정의되어 있다.
- x보다 크고 x와 비트가 1 ~ 2개 다른 수들 중에서 제일 작은 수
예를 들어,
f(2) = 3 이다.
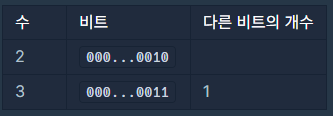
아래의 표와 같이 2보다 큰 수들 중에서
비트가 다른 지점이 2개 이하이면서 제일 작은 수는 3이기 때문이다.
f(7) = 11이다.
아래의 표와 같이 7보다 큰 수들 중에서
비트가 다른 지점이 2개 이하이면서 제일 작은 수는 11이기 때문이다.

정수가 담긴 배열 numbers가 매개변수로 주어지는 경우,
number의 모든 수들에 대하여 각 수의 f 값을 배열에 차례대로 담아서 return 하시오.
제한사항
1 <= numbers의 길이 <= 100,000
0 <= numbers의 모든 수 <= 10^15
이 문제는 비트 연산과 연결된 문제로 접근하는 방법이 다양하다고 생각한다.
우선은 통과한 답은 아래의 코드이다.
using System;
public class Solution {
public long[] solution(long[] numbers) {
long[] answer = new long[numbers.Length];
for (int i = 0; i < numbers.Length; i++)
{
long number = numbers[i];
if ((number & 1) == 0) // 짝수인 경우
{
answer[i] = number + 1;
}
else
{
long m = number + 1;
answer[i] = number + (m & -m) / 2;
}
}
return answer;
}
}
이 코드를 설명하기 전에 C#에서 사용하는 비트 연산에 대해 알아보면
비트 및 시프트 연산자 - 정수 형식의 개별 비트에서 부울(AND, NOT, OR, XOR) 및 시프트 연산 수행 - C#
정수 계열 형식의 피연산자를 사용하여 비트 논리(AND - '&', NOT - '~', OR - '|', XOR - '^') 또는 shift 연산('<<' 및 '>>')을 수행하는 C# 연산자에 대해 알아봅니다.
learn.microsoft.com
비트 연산
1. 시프트 연산자 (<<, >>)
시프트 연산자는 비트를 왼쪽이나 오른쪽으로 이동시키는 연산으로
2의 거듭제곱으로 곱하거나 나누는 연산이다.
2. AND 연산
두 개의 비트가 1인 경우에만 1을 반환하고 그 외에는 0을 반환한다.
3. OR 연산
두 개의 비트 중 하나라도 1이라면 1로 반환하고, 두 비트가 모두 0인 경우에만 0을 반환한다.
4. XOR 연산
두 개의 비트가 값이 같으면 0을, 다르면 1을 반환한다.
5. NOT 연산
비트 값을 반전시켜 반환한다.
시도했던 풀이 방법
문제를 풀면서 마지막 10번, 11번 문제에서 시간초과가 났었지만 문제해결에서 사용할 수 있는 방법이었던
HammingDistance(해밍 거리) 방법도 있었다.
이 부분에 대해 정리하면,
해밍 거리란 이진 표현 사이에서 서로 다른 위치의 개수를 측정하는데 사용하는 방법이다.
예를 들어서 두 이진수 '1011101'과 '1001001'의 해밍 거리를 계산하면,
두 이진수의 차이는 세번째와 다섯번째의 차이로, 이들의 해밍 거리는 2가 된다.
해밍 거리를 계산하는 코드는 아래와 같다.
int HammingDistance(int a, int b) {
int xor = a ^ b;
int distance = 0;
while (xor != 0) {
distance += xor & 1;
xor >>= 1;
}
return distance;
}
위의 코드에서 a와 b 사이의 해밍 거리를 계산하는데, xor은 두 입력이 다를 때 1을 반환하므로,
xor의 결과에서 1의 개수를 세면 해밍 거리를 구할 수 있다.
이를 이용하여 처음에 시도했던 답안은 아래와 같다.
using System;
public class Solution {
public long[] solution(long[] numbers) {
long[] answer = new long[numbers.Length];
for (int i = 0; i < numbers.Length; i++)
{
answer[i] = HammingNumber(numbers[i]);
}
return answer;
}
static public long HammingNumber(long a)
{
long tmp = a + 1;
while (true)
{
long xor = a ^ tmp;
int distance = 0;
while (xor != 0)
{
distance += (int)(xor & 1);
xor >>= 1;
}
if (distance <= 2)
{
return tmp;
}
tmp++;
}
}
}
이 문제에서 만약 숫자의 범위가 long이 아닌 int였다면 사용할 수 있었던 답안이지만,
숫자의 크기가 너무 커져서 문제에서 시간초과로 풀지 못하는 문항이 있었다.
정답 코드 분석
위의 방법으로는 해결하지 못하는 큰 수를 해결하기 위해서 해밍 거리를 구하는 방식이 아닌,
숫자들의 특성을 이용해서 문제를 풀게되었다.
이 경우에는 숫자가 짝수인지 홀수인지에 따라서 전략이 달라지는데,
짝수라면 이진수로 표현했을 때, 마지막 자리수가 0이기 때문이다.
예를 들어서 2 = 10, 4 = 100, 6 = 110, 8 = 1000, 10 = 1010, 12= 1100, ... 으로
2의 거듭제곱으로 표현하는 이진수의 마지막 자리수는 1을 나타내므로, 짝수의 경우에는 항상 마지막 자리수는 0이다.
따라서 짝수의 경우에는 원래 숫자에 1을 더하면 문제에서 원하는 f(x)의 값을 구할 수 있다.
if ((number & 1) == 0) // 짝수인 경우
{
answer[i] = number + 1;
}
다음으로 홀수인 경우를 계산해보면,
홀수에서 1을 더하면 짝수가 되므로 이를 먼저 구한 뒤에
이를 가지고 거리가 2이하인 숫자를 구하는데 우선 코드를 적으면 아래와 같다.
else
{
long m = number + 1;
answer[i] = number + (m & -m) / 2;
}
여기서 number는 홀수이므로 m은 짝수이다.
다음으로 (m & -m) / 2가 중요한데,
-m의 경우에는 2의 보수를 이용하여 표현하며, m의 모든 비트를 반전시킨 다음 1을 더함으로써 얻어진다.
예를 들어 m은 8인 경우에 이진수로 표현하면 1000인데 여기서 모든 비트를 반전시키면 0111이 되고,
여기에 1을 더하면 1000이 된다. 즉, -8의 2의 보수 표현은 1000으로
m이 8일때 (m & -m)은 1000이고 2로 나눈 값은 4로 0100이다.
여기서 원래 7(0111)에 4(0100)를 더한 11(1011)로 원래의 이진 표현에서 비트가 2개가 달라진 것을 확인할 수 있다.
이를 정리하면 (m & -m)를 통해서 m에서 가장 낮은 비트(1)의 위치를 찾아내고
이를 2로 나눠주어 해밍 거리가 2 이하를 만족하는 가장 작은 수를 찾을 수 있게 된다.
오늘은 알고리즘 문제를 풀면서 비트와 연관된 문제를 풀게되어 비트 연산에 대해서 정리하는 시간을 가졌다.
전문적인 지식이 많이 필요한 부분이라 아직은 정확히 이해되지 않았지만,
해밍 거리라는 개념을 도입하고 문제를 풀어보면서 조금은 익숙해질 수 있는 기회가 되었다고 생각하고
추후에도 몇 번 비슷한 문제를 풀면서 정리하면 조금 더 내 것으로 만들 수 있을 것이라고 생각한다.
'IT > TIL' 카테고리의 다른 글
| 20240214_오브젝트 풀링 (0) | 2024.02.14 |
|---|---|
| 20240213_오버로딩, 오버라이딩 (0) | 2024.02.14 |
| 20240209_유니티 초기화 순서 관련 (0) | 2024.02.10 |
| 20240208_기술면접 회고 (1) | 2024.02.09 |
| 20240207_유니티 상속 관련 (0) | 2024.02.07 |