2024. 2. 6. 22:47ㆍIT/TIL
오늘의 TIL은 프로그래머스의 문제인 멀쩡한 사각형에 관한 내용이다.
문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/62048
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제에 대해서 설명하면
가로의 길이가 W cm, 세로의 길이가 H cm인 직사각형 종이가 있을 때,
이 직사각형을 이루는 1cm X 1cm의 정사각형이 꽉 차 있을 때,
이 종이의 대각선 꼭지점 2개를 잇는 방향으로 잘라놓았을 때,
이 종이에서 사용할 수 있는 1cm X 1cm의 정사각형의 개수를 찾는 문제이다.
제한 사항
W, H : 1억 이하의 자연수
예시 설명
아래의 사진처럼 가로가 8, 세로가 12인 직사각형을 대각선 방향으로 자르면
총 16개의 정사각형을 사용할 수 없게 되므로,
원래 직사각형의 96개 에서 16개를 빼면 80개가 사용할 수 있는 정사각형의 개수이다.

통과한 답
using System;
public class Solution {
public long solution(int w, int h) {
long answer = 0;
answer = ((long)w * (long)h - w - h + GCD(w, h));
return answer;
}
static private int GCD(int w, int h)
{
while (h != 0)
{
int tmp = h;
h = w % h;
w = tmp;
}
return w;
}
}
문제의 풀이 전략은 예시에서 주어진 것과 같은 방식인데,
총 정사각형의 개수에서 대각선 꼭지점이 지나가는 정사각형의 개수를 빼는 방식이다.
따라서 이 문제는 매우 수학적인 문제로 변경할 수 있는데,
좌표평면 상에서 (W, 0), (0, H)를 지나는 직선이 지나가는 정사각형의 개수를 구하면 된다.
다시 말해서, 이 직선의 시작점과 끝점 사이에 있는 격자점의 수를 세면 되는데,
이 격자점의 수는 시작점과 끝점 사이의 격자점의 수에 기반하고
시작점과 끝점의 좌표를 사용하여 두 점 사이의 격자점의 수를 계산할 수 있으며
이는 두 점의 x좌표 차이와 y좌표 차이의 최대공약수(GCD)와 관련이 있다.
(W, 0), (0, H)를 지나는 직선은 Hx + Wy = WH 이며 직선의 기울기는 - H / W 이다.
직선이 지나는 정사각형의 총 수를 계산하는 방법은 직선이 교차하는 격자점의 수와 관련이 있으며,
이는 시작점과 끝점 사이의 최대공약수(GCD)로 표시할 수 있다.
이를 표현하면 직선이 지나는 정사각형의 총 수는 W + H - GCD(W, H)로 계산할 수 있다.
직선이 지나가는 각 격자 영역은 W번과 H번이므로, W + H를 해주고
겹치는 부분은 W와 H의 최대공약수 이므로 GCD(W, H)를 빼주는 것이다.
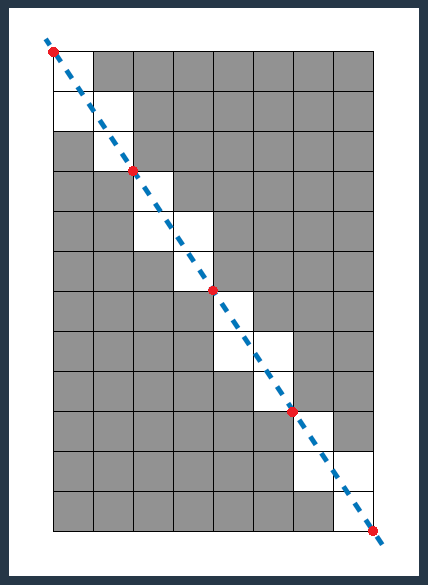
위의 이미지에서 H = 8, W = 12인 경우에 격자점은 5개가 생성되며,
이 직선이 통과하는 격자점의 수는 4개(처음과 끝을 뺀 3개 + 처음과 끝을 하나로 만들어서 1개)이므로,
이 직선이 통과하는 정사각형의 개수는 W + H - GCD(W, H)로 8 + 12 - (GCD(8, 12) = 4)가 된다.
따라서 이를 코드로 작성하면 아래와 같다.
using System;
public class Solution {
public long solution(int w, int h) {
long answer = 0;
answer = ((long)w * (long)h - w - h + GCD(w, h));
return answer;
}
static private int GCD(int w, int h)
{
while (h != 0)
{
int tmp = h;
h = w % h;
w = tmp;
}
return w;
}
}
단, 여기서 주의해야할 점은 W와 H가 1억 이하의 자연수이므로
이들의 곱은 int의 범위를 초과하는 경우가 있을 수 있으므로 앞에 long으로 명시해줘야한다.
(answer가 long 이라는 것도 힌트가 될 수 있다)
오늘은 알고리즘 문제를 풀면서 코딩쪽의 영역보다는 수학적인 영역에 기반하여 문제를 풀었는데,
알고리즘 문제뿐만 아니라 실제로 게임을 만드는 과정에서도 수학이 사용되는 경우가 많다고 느끼고 있다.
따라서 이를 포기하고 넘어가는 것이 아니라 나올 때마다 이를 해결할 수 있도록
수학적으로도 공부를 꾸준히 해야될 것으로 느꼈다.
'IT > TIL' 카테고리의 다른 글
| 20240207_유니티 상속 관련 (0) | 2024.02.07 |
|---|---|
| 20240207_삼각 달팽이(프로그래머스) (0) | 2024.02.07 |
| 20240205_SOLID원칙 (0) | 2024.02.05 |
| 20240204_마법의 엘리베이터(프로그래머스) (0) | 2024.02.05 |
| 20240203_최종프로젝트 트러블슈팅 (2) | 2024.02.03 |